Автор конспекта:
Автор(ы): — Осипцова Галина Петровна
Место работы, должность: —
МБОУ "Средняя общеобразовательная школа №12" города Выборга, учитель математики.
Регион: — Ленинградская область
Характеристики урока (занятия) Уровень образования: — среднее (полное) общее образование
Целевая аудитория: — Учитель (преподаватель)
Класс(ы): — 11 класс
Предмет(ы): — Алгебра
Предмет(ы): — Математика
Цель урока: —
Сформировать умение применять производную к исследованию функций и построению графиков.
Развивать логическое мышление, умение анализировать, умениеставить проблему, решать ее.
Воспитывать желание высказывать свое мнение.
Тип урока: — Урок изучения и первичного закрепления новых знаний
Учеников в классе: — 27
Используемые учебники и учебные пособия: —
УМК: С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин
Используемая методическая литература: —
М.К. Потапов, А.В.Шевкин "Алгебра и начала математического анализа, 10". Книга для учителя. М: "Просвещение" 2010.
Используемое оборудование: —
Компьютер, документ камера, таблица с алгоритмом исследования функции, карточки с заданиями.
Краткое описание: —
Урок алгебры и начал анализа в 11 классе
(УМК: С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин)
Тема урока: «Применение производной к построению графиков функций»
Основные цели урока:
сформировать умение применять производную к исследованию функций и построению графиков;
развивать умение ставить проблему, решать ее, логическое мышление, умение анализировать;
воспитывать желание высказывать свое мнение.
Оборудование и раздаточный материал: компьютер, документ камера, таблица с алгоритмом исследования функции, карточки с заданиями.
Ход урока
Мотивация учебной деятельности.
- Здравствуйте, ребята.
- Что нового вы узнали на предыдущих уроках? (как с помощью производной найти критические точки, промежутки возрастания, убывания функции, ее экстремумы, наибольшее ( наименьшее) значение).
- На этом уроке мы продолжим исследовать функции с помощью производной.
Актуализация знаний.
На экране вы видите график функции y = f (x):
- Какие свойства функции можно определить по графику? Назовите их.
Ответ: 1) D(f) = R;
2) функция непрерывна
3) Функция возрастает на отрезке [-2; 0,5] и на промежутке [3; +∞), а значит, f '(x) > 0 на (-2; 0,5) и на (3; +∞).
Убывает на (-∞; -2] и на [0,5; 3], а, значит, f '(x) < 0 на (-∞; -2) и на (0,5; 3).
точки максимума функции:x точки минимума: x = -2 x = 3;
4)наибольшее значение функции не существует, наименьшее равно-2 при = 3;
E(f) = [-2; +∞).
- Как найти точки экстремумов функции? (Если производная при переходе через критическую точку меняет знак с «+» на «-», то данная точка является точкой максимума, если же производная при переходе через критическую точку меняет знак с
«-»на «+», то данная точка является точкой минимума, если производная при переходе через критическую точку знак не меняет, то данная критическая точка не является точкой экстремума.
− Сформулируйте алгоритм нахождения промежутков возрастания, убывания и экстремумов функции у = f(x), заданной аналитически.
Учащиеся формулируют, на экране последовательно открываются шаги алгоритма.
Алгоритм.
1. Найти область определения функции.
2. Найти производную функции.
3. Найти критические точки.
4. Отметить на числовой прямой область определения и критические точки. Пользуясь обобщенным методом интервалов, определить знаки производной на полученных промежутках.
5. Пользуясь достаточными признаками, найти промежутки возрастания, убывания и экстремумы функции.
- А теперь исследуйте функцию f(x) =⅓x³ + 2x² + 3x.
Учитель записывает на доске под диктовку учащихся. Учащиеся работают в тетрадях.
Функция ни четная, ни нечетная, непериодическая.
Точки пересечения
с осью х: (0; 0) и (-3; 0), т. к.
f(x) = 0, т. е. ⅓x³ + 2x² + 3x = 0
⅓x (x² + 6 x + 9) = 0
⅓x (х + 3)² = 0
х = 0; х = -3
с осью у: (0; 0).
Производная функции:f'(x) = x² + 4х + 3, D(f '(x)) =R
критические точки: f '(x) = 0 при х = -3, х = -1.
Отмечаем на числовой прямой критические точки и определяем знаки производной на полученных промежутках:
f '(x) > 0 на (-∞; -3) и на (-1; +∞); f '(x) < 0на (-3; -1), значит, f(x) возрастает на (-∞; -3] и на [-1; +∞), убывает на [-3; -1].
fmax = 0 при х = -3, fmin = -4 при х = -1
4) Наибольшего и наименьшего значений функция не имеет.
5) E(f)= R
— Что вы повторили?
.
- Как вы думаете, какое следующее задание я вам предложу?
- Итак, вы провели исследование функции. А теперь вам надо, используя результаты исследования, построить график функции f(x) =⅓x³ + 2x² + 3x.
Возникнут ли у вас затруднения?
3. Выявление затруднений, проблемы
Учитель предлагает нескольким учащимся озвучить затруднения.
- Какое задание вы должны были выполнить? (Используя данные исследования, построить график функции).
- Почему у вас возникли затруднения? (Не знаем способа построения графиков по данным исследования функции).
- Что вы используете для исследования функции? (Производную).
4. Построение проекта выхода из затруднения.
- Сформулируйте цель вашей деятельности. (Узнать способ построения графика, используя исследование функций с помощью производной).
- Сформулируйте тему урока. ( Применение производной для построения графиков функций).
Тема урока открывается на доске.
- Итак, у вас возникло затруднение при построении графика функции. Что вы раньше использовали для построения графиков функций? ( таблицы с некоторыми точками, принадлежащими графику).
- Но часто точки не дают объективной картинки графика. И теперь, зная алгоритм исследования функции, какие данные будете вносить в таблицу? (нужно внести в таблицу результаты исследования функции, затем по таблице построить график).
5. Реализация построенного проекта
На доске открывается пустая таблица:
х
f(x)
f '(x)
- Вы исследовали функцию f(x) =⅓x³ + 2x² + 3x.
Перечислите шаги, которые вы выполняли при исследовании функции.( По ходу заполняется таблица)
х
(-∞; -3)
- 3
(-3; -1)
-1
(-1; + ∞)
f '(x)
+
0
_
0
+
f(x)

0

-4

max
min
- Результаты, полученные в таблице, переносим на координатную плоскость.
Что еще можно сделать, чтобы более точно построить график? (Можно найти несколько дополнительных точек, принадлежащих графику функции).
На доске появляется график функции f(x) =⅓x³ + 2x² + 3x.
- Вы построили график функции.
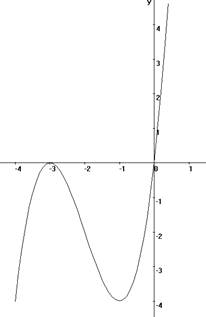
Как вы это сделали? (Мы создали алгоритм построения графика). (Еще раз проговариваем этапы исследования функции и построения ее графика).
Алгоритм построения графика с помощью производной..
таблица
дополнительные точки;
график.
6. Первичное закрепление приобретенных знаний.
- Что теперь необходимо сделать? ( надо научиться использовать алгоритм для построения графиков).
— Постройте теперь график функции . f(x) = х +

.
Один ученик работает у доски, комментируя свои действия, остальные работают в тетрадях.
D(f ') = (-∞; 0) U (0; + ∞).
Критические точки: = 0 при х = 2 и х = -2, точек, в которых f'() не существует – нет.
Таблица:
x
(-∞; -2)
-2
(-2; 0)
0
(0; 2)
2
(2; + ∞)
f '(x)
+
0
-
нет
-
0
+
f(x)

-4

нет

4

max
нет
min
5. Дополнительные точки:
x
1
4
y
5
5
6. График функции:
- Попытайтесь изобразить график самостоятельно.
На экране появляется график для проверки.
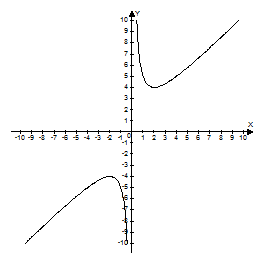
7. Самостоятельная работа с самопроверкой по образцу
– А теперь давайте проверим, как каждый из вас понял, как применять построенный алгоритм.
Вариант 1.
Исследовать функцию и построить ее график
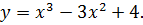
Вариант 2.
По частично проведенному исследованию построить график функции

Учащиеся выполняют задание самостоятельно, после выполнения работы учащиеся сопоставляют свои работы с подробным образцом:
Вариант 1.
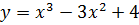
1) D (f) = R, функция непрерывна.
2) y| = 3×2 – 6x
3) 3×2 – 6x = 0; D (f|) = R
х1 = 0; х2 = 2
4)
х
(− ¥; 0)
0
(0; 2)
2
(2; +¥)
¦/(х)
+
0
−
0
+
¦(х)

¦(0) = 4

¦(2) = 0

max
min
6) график
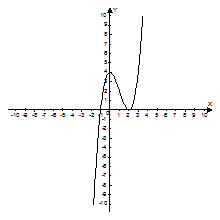
Вариант 2.
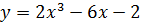
1) D (f) = R, функция непрерывна.
2) y¢ = 6×2 – 6
3) 6×2 – 6 = 0; D (f|) = R
х1 = − 1; х2 = 1
+ − +

− 1 1
4)
x
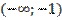
-1
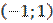
1
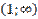
f’(x)
+
0
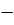
0
+
f(x)

2

-6

max
min
− У кого задание вызвало затруднение?
− На каком шаге алгоритма?
− В чем причина возникшего затруднения?
− У кого задание выполнено правильно?
8. Включение в систему знаний и повторение.
– Давайте теперь посмотрим, в каких заданиях ЕГЭ можно применить полученные знания.
Решите задачи:
1. Найдите множество значений функции
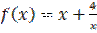
.
2. При каких значениях параметра р уравнение
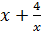
= p имеет 2 корня, 1 корень, не имеет корней?
1) Ответ : (− ¥; − 4]U [4; + ¥).
2) Ответ: 2 корня при р4; 1 корень при р = − 4 и р = 4; не имеет корней при − 4< p
